FUNKCJE

Funkcja – intuicyjnie: sposób przyporządkowania każdemu elementowi danego zbioru X dokładnie jednego elementu pewnego zbioru Y.

Ściśle funkcja jest definiowana jako relacja pomiędzy elementami zbioru $X$ (dziedziny) i elementami zbioru $Y$ (przeciwdziedziny), o tej własności, że każdy element zbioru $X$ jest w relacji z jednym i tylko jednym elementem zbioru $Y$ .

Przykłady

Załóżmy, że między dwoma liczbami całkowitymi x i y zachodzi związek y = 2x. Ta zależność pozwala jednoznacznie wyznaczyć y mając dany x, np. dla x = 5 mamy y = 10, dla x = 2 mamy y = 4. Jest to zatem funkcja.

Każda funkcja przyporządkowuje argumentom (tutaj oznaczanym x) odpowiadające im wartości (tutaj oznaczane y). Oznaczając funkcję literą f, wartość dla argumentu x zapisuje się f(x) (czyt. "f od x")^[1]. Tak więc dla argumentu 5 wartością funkcji f jest 10, czyli f(5) = 10.

Dziedziną funkcji nazywa się zbiór wszystkich argumentów, a zbiorem wartości zbiór wszystkich wartości przyjmowanych przez funkcję; w tym przykładzie dziedziną jest zbiór liczb całkowitych, a zbiorem wartości zbiór liczb parzystych. Często wymaga się podania przeciwdziedziny, która zawiera zbiór wartości, lecz nie musi być mu równa^[2]. Jeżeli w przykładzie za przeciwdziedzinę obierzemy zbiór liczb całkowitych, to liczby nieparzyste nie będą w zbiorze wartości.

Zdanie "f jest funkcją o dziedzinie X i przeciwdziedzinie Y" zapisuje się $f\colon X \to Y$ , zbiór wszystkich funkcji $X \to Y$ zapisuje się Y^X.

Funkcje nie muszą odnosić się do liczb. Przykłady:

przyporządkowanie każdemu ciału fizycznemu jego środka ciężkości,
przyporządkowanie każdemu mieszkańcowi miasta jego pierwszego imienia,
symetria względem prostej,
symetria względem punktu.

Nazwa

W matematyce określenia: funkcja, przekształcenie, odwzorowanie, transformacja, operator, działanie, itd. są zwykle synonimami. Jednakże w różnych dyscyplinach matematycznych preferowane jest używanie niektórych z nich, znaczenie niektórych zostało zaś zawężone. Użycie konkretnej nazwy podyktowane jest dzisiaj przede wszystkim względami historycznymi.

Choć w analizie matematycznej rozpatruje się przede wszystkim funkcje, to w geometrii, algebrze liniowej mówi się o przekształceniach (przekształceniach liniowych), w algebrze uniwersalnej rozważa się z kolei działania, zaś w analizie funkcjonalnej bada się własności operatorów, czy funkcjonałów.

Sposoby określenia funkcji

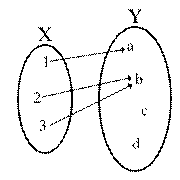
Funkcja przedstawiona jako graf. Każdemu argumentowi ze zbioru X przyporządkowano dokładnie jeden element ze zbioru Y. Dwóm różnym elementom w X może odpowiadać ten sam element Y. Nie każdy element zbioru Y musi być wartością funkcji.

Jeżeli dziedzina X jest skończona, wystarczy wymienić wszystkie pary argument – wartość. Można to zrobić za pomocą grafu (przykład obok).Najczęściej funkcje definiuje się wzorem lub ogólniej – algorytmem, tj. metodą pozwalającą znaleźć f(x) dla danego $x \in X$ . Możliwe jest użycie rekursji, rozwinięcia w szereg potęgowy itp. Oczywiście powyższe metody nie wykluczają opisu słownego, który bywa niekiedy wygodniejszy, np. "każdej liczbie całkowitej dodatniej n przyporządkowujemy n-tą liczbę pierwszą". W matematyce stosowanej funkcje często określa się za pomocą tabeli lub wykresu. Nie pozwala to na ogół ustalić dokładnej zależności, lecz przy pewnych założeniach możliwa jest ich interpolacja (przybliżanie), całkowanie numeryczne itp.

Rodzaje

Niektóre szczególne rodzaje funkcji wraz z nieścisłym opisem:

funkcje monotoniczne – wartości dla kolejnych argumentów są coraz większe, mniejsze, nie mniejsze, nie większe lub stałe,
funkcje ograniczone – zbiór wartości jest ograniczony,
funkcje parzyste i nieparzyste – wykres jest symetryczny względem osi $OY$ bądź początku układu współrzędnych;
funkcje okresowe – wartości "powtarzają się" co pewną ustaloną wartość nazwaną okresem,
funkcje ciągłe – można nakreślić ich wykres bez odrywania ołówka od kartki,
funkcje różniczkowalne - mające pochodną w każdym punkcie swojej dziedziny.

Zobacz też: funkcje elementarne, funkcje specjalne, badanie przebiegu zmienności funkcji

Definicja formalna

Nieformalna definicja funkcji jako przyporządkowania jest używana również dzisiaj, np. w podręcznikach wprowadzających do analizy matematycznej. Jest ona wystarczająca dla dużej liczby zastosowań, lecz używa pojęcia "przyporządkowania", którego sens trudno oddać w ścisły sposób.

Funkcją ze zbioru X w zbiór Y nazywa się podzbiór iloczynu kartezjańskiego $W \subset X \times Y$ (relację dwuargumentową) spełniający warunki

$\forall_{x \in X}\; \exists_{y \in Y}\; x\ f\ y$ ,

$\forall_{x \in X}\; \forall_{y \in Y}\; \forall_{z \in Y}\; x\ f\ y \and x\ f\ z \implies y = z$ ,

czyli

każdy element zbioru X musi być w relacji z dokładnie jednym elementem zbioru Y.

Zbiór X nazywa się dziedziną funkcji, zbiór Y jej przeciwdziedziną. Zbiór W nazywa się wykresem funkcji.

Jeżeli $x \in X, (x,y)\in W$ to mówimy, że wartością funkcji dla x jest y, co zapisuje się f(x) = y. Z definicji wynika, że y jest wyznaczone jednoznacznie. Dla $x \notin X$ symbol f(x) jest nieokreślony.

Przy określaniu funkcji należy podać przeciwdziedzinę, ponieważ nie wyznacza jej zbiór W. Jednak często (np. w teorii mnogości) funkcje i ich wykresy są utożsamiane; wówczas podanie przeciwdziedziny nie jest wymagane. Niekiedy funkcję definiuje się jako trójkę uporządkowaną $(X,\; Y,\; f)$ ; przy takiej definicji, funkcje o różnych przeciwdziedzinach są różne.

Funkcje jako struktury

Funkcje odgrywają ważną rolę w matematyce jako środki pomocnicze do tworzenia większych struktur (układów).

Przykład

Zapiszmy liczby 4,5,6,7 w tabeli $2 \times 2$ .

$\begin{pmatrix} 4 & 5\\ 6 & 7\\ \end{pmatrix}$

Taką tabelę można przedstawić w postaci funkcji, która przyporządkowuje każdemu miejscu w tabeli jedną z liczb. Poszczególne miejsca będą reprezentowane jako pary (i,j) oznaczające numer wiersza i kolumny:

$(2, 1) \mapsto 6$

Ogólnie każdą taką tabelę można zapisać w postaci funkcji

$\{(1, 1),\ (1, 2),\ (2, 1),\ (2, 2)\} \to \mathbb R,\quad (i,j )\mapsto a_{ij}$

wtedy będą znajdować się w niej liczby a₁₁, a₁₂, a₂₁ i a₂₂.

W taki sposób definiuje się obiekty takie jak ciągi i macierze. Należy pamiętać o różnicach w nomenklaturze: mimo że ciągi i macierze są funkcjami, to mówi się o "wyrazach" i "wskaźnikach", a nie "wartościach" i "argumentach" ciągu, "elementach", a nie "wartościach" macierzy.

Rys historyczny

Poszukiwaniem wzajemnych zależności między różnymi wielkościami zajmowali się już starożytni Grecy, jednak pierwszą ogólną definicję funkcji podał dopiero w 1718 r. matematyk szwajcarski Jan Bernoulli.

Pełną definicję funkcji (jako przyporządkowania) pierwszy sformułował matematyk niemiecki Peter Gustav Lejeune Dirichlet w 1837 r. Dzisiaj pojęcie funkcji jest jednym z najważniejszych pojęć matematyki.

Moje strony:

Chemia

Informatyka

Geografia

Strony kolegów:

Tomek S.

Kuba J.

Rafał D.